Руководство по ATB-шкале
Автор - Einwill. Предыдущая версия «Руководства» была написана игроком Noldor на основе статьи с Геройского уголка. Изложенные ниже принципы дискретной ATB-шкалы ГВД были «открыты» игроком Сойот.
ATB (от англ. Active Time Battle - сражение с периодами активности) — это применяемая в компьютерных играх система боёв, служащая альтернативой простому пошаговому сражению. Эта система пытается приблизить ход боя к «непрерывному» течению времени, делая сражение более динамичным. При этом бой по-прежнему остаётся тактическим действием: игра не превращается в простую «стрелялку». В серии Героев ATB-система боев появилась лишь в 5-й части, и с некоторыми изменениями перекочевала оттуда в мир ГВД.
Интуитивно эта система выглядит простой и понятной: под полем битвы расположена линейка инициативы (так называемая внешняя ATB-шкала), на которой показано, в каком порядке отряды на поле боя получат право хода. Чем шустрее отряд, т.е., чем выше у него параметр «Инициатива», тем чаще он появляется на этой линейке ходов.
Игроки быстро привыкают к такой манере боя. И лишь со временем у них появляются естественные вопросы: «Как отделить от стека единичку так, чтобы единичка ходила первой?», «Почему мой юнит с ини 11 сделал первых ход позже юнита с ини 10?», «Что означает время действия того или иного заклинания?» и т.д. Чтобы ответить на подобные вопросы, надо разобраться в механизме, по которому формируется эта линейка инициативы. А формируется она при помощи так называемой внутренней ATB-шкалы, про которую и пойдёт речь в нашей статье.
Мысленно (внутреннюю) АТВ-шкалу можно представить как стадион с длиной круга 100 метров. Юниты бегут по нему со скоростью, равной их инициативе: например, минотавры с инициативой 8 бегут со скоростью 8 м/с и пробегают весь круг за 12.5 секунд. Когда, сделав полный круг, отряд пересекает линию старта/финиша, ему предоставляется право хода в игре.
Как видите, всё довольно просто. Весь этот механизм скрыт от игрока, необходимые вычисления выполняет компьютер: он прогоняет все юниты на несколько кругов вперёд по ATB-шкале, запоминает в каком порядке они пересекают финишную черту, и отображает этот порядок ходов на линейке инициативы.
Различные события на поле боя — выпавшая мораль, применение различных заклинаний (ускорение/замедление) или спец.способностей юнитов и героев (отбрасывающий удар и т.п.) — могут изменять положение и скорость движения отряда по ATB-шкале. Например, если отряду после хода выпадает моралька, то он «телепортируется» в середину круга, тем самым вдвое сокращается дистанция, которую ему надо пробежать: в итоге следующий ход отряда наступает в два раза быстрее.
Ниже механика движения по ATB-шкале будет описано подробно, а пока обратим внимание на некоторые особенности ATB-шкалы в ГВД.
Проведение боёв в ГВД содержит несколько особенностей, скрытых в механизме ATB-шкалы. Незнание этих особенностей часто приводит новичков к непониманию почему то-то и то-то произошло в их бою, им кажется, что это «баг», ошибка игры, что такого не должно быть. Поэтому, прежде чем двигаться дальше в исследовании ATB-шкалы, мы подробно опишем эти особенности.
3.1. Размещение отрядов в начале боя
Если бы в начале боя все существа на внутренней ATB-шкале стартовали вместе, одновременно, то право первого хода всегда получало существо с самой большой «скоростью» (т.е. с самой высокой инициативой). Создателям 5-х героев, да и администраторам ГВД, показалось, что такая предсказуемость сделает бои неинтересными. И то правда: стоит на 1% поднять инициативу: и вот уже твои лучники гарантированно опережают лучников противника. Сражения станут динамичнее, если первый ход будет случайно доставаться тому или иному отряду; но, разумеется, шансы пойти первым должны быть тем больше, чем выше параметр Инициативы.
Именно так и обстоят дела в ГВД. Достигается это очень простым способом: в начале боя все отряды сдвигаются со старта ATB-шкалы на случайное расстояние — от 0 до 10 «метров». К чему это приводит? Давайте разберёмся на примере:
Пусть в бою участвуют орки с инициативой 11 и эльфийские лучники с инициативой 10. Если бы они начинали свой «забег» на внутренней ATB-шкале со старта, то, конечно, первыми к финишу пришли бы орки. Но пусть стартовый разброс поместил орков в точку 0 (самое начало круга), а эльфов отправил в точку 10. Тогда, как не сложно понять, орки не смогут до конца первого круга отыграть гандикап. Действительно, эльфам-лучникам надо пробежать 90 метров, чтобы достигнуть финиша. Они сделают это за 90/10 = 9 секунд. За это время орки пробегут 9*11 = 99 метров. В итоге, через 9 секунд орки будут в точке 0+99 = 99, а эльфы-лучники в точке 10+90 = 100, т.е. они первыми пробегут полный круг и получат право хода. И эльфийские лучники с ини 10 пойдут раньше орков с ини 11: вот такие чудеса.
Следует отметить, что ини орков всё же сыграет им на руку: нехитрые подсчёты показывают, что уже на втором круге нашего ATB-стадиона орки обгонят лучников и получат следующий ход раньше их (ведь дальше все отряды продолжают бежать уже без всяких дополнительных бонусов). В итоге (если забыть обо всех других юнитах на поле), внешняя ATB-шкала будет выглядеть так: Эльфы-лучники, Орки, Орки, Эльфы-лучники…
Также не стоит забывать, что на деле шансы эльфов-лучников опередить орков весьма малы. Ведь при подавляющем большинстве начальных разбросов, даже оказавшись в момент старта позади эльфов, орки сумеют обогнать их ещё до конца первого круга, и первыми получат право хода.
Итак, из-за случайного разброса отрядов на ATB-шкале в начале боя, превосходство в Инициативе не всегда гарантирует первенство хода в бою. Но, чем выше Инициатива, тем больше шансов пойти первым. Ниже мы ещё поговорим об этом подробнее, а пока вернёмся к описанию особенности реализации ATB-шкалы в ГВД.
3.2. Дискретность ATB-шкалы
В ГВД используется дискретная ATB-шкала, в отличие от непрерывной ATB-шкалы в пятых Героях. Как мы вскоре увидим, различие это весьма существенно.
Дискретность ATB-шкалы проявляется и в расстояниях, и во времени. Расстояния градируются дециметрами; т.е. на ATB-шкале есть, например, точки 1 метр, 1.2 метра, но нет точки 1.25. Время же измеряется только в целых секундах: на нашем ATB-стадионе может пройти 2 или 3 секунды, но не 2.5.
Мысленно эту дискретность можно представить примерно следующим образом: весь «забег» отрядов на стадионе записывается на камеру наружного наблюдения. Камера имеет плохое разрешение и на ней нельзя различить мелкие объекты. Кроме того «снимки» камера делает лишь раз в секунду. В итоге, просматривая забег, снятый такой камерой, мы видим, как отряды скачками передвигаются по стадиону. На предыдущем кадре отряд был на старте, а на следующем уже скакнул на 9 метров вперёд — и что происходило в промежутке между этими кадрами мы не знаем.
Дискретность расстояний не оказывает особого влияния на игру. По большому счету, она лишь делает дискретным инициативу юнитов. Например, Арбалетчики (базовая ини 8) с бонусом 7% к инициативе от артов/статов/гильдий будут иметь итоговую инициативу не 8*1.07 = 8.56, а округлённую 8.6 (ведь на нашей ATB-шкале нет расстояния 8.56, и за секунду его не пробежать). А вот дискретность времени имеет гораздо более серьёзные последствия. Чтобы убедиться в этом, давайте рассмотрим следующий пример:
Пусть эти самые Арбалетчики с инициативой 8.6 пошли охотиться на Огненных элементалей (базовая ини 8). Пусть начальный разброс поместил Арбалетчиков в точку 3 (метра), а Элементалей — в точку 10. Давайте определим, кто из них выстрелит первым. Это не сложно: расчёты на ATB-шкале напоминают решение простеньких задач их курса школьной физики.
Сначала произведём расчёты для непрерывной ATB-шкалы (которая, например, использовалась в пятых Героях). Арбалетчикам надо преодолеть 97 метров до финиша, сделают они это за 97/8.6 = 11.279… секунд. Элементалям же потребуется «пробежать» лишь 90 метров, и на это у них уйдёт 90/8 = 11.25 секунд. Как видим, Огненным элементалям понадобится меньше времени, чтобы добежать до линии старта/финиша, поэтому они раньше арбалетчиков получат право хода.
А теперь посмотрим, что происходит на нашей дискретной ATB-шкале. В начальные боя Арбалетчики стоят в точке 3, а Элементали — в точке 10. Через секунду картинка меняется: Арбалетчики «перепрыгивают» в точку 3+8.6 = 11.6, а Элементали оказываются в точке 10+8 = 18. Подобные «кадры» будут сменять друг-друга; и через 11 секунд Арбалетчики достигнут точки 3+8.6*11 = 97.6 и почти догонят Элементалей: те будут в точке 10+8*11 = 98. Итак, оба отряда уже вплотную подбежали к финишу (отметке 100). Но мы не узнаем кто из них пересек финиш первым, ибо нам будет доступен только «снимок» сделанный на следующей, 12й секунде. А к этому времени оба отряда уже пробегут мимо финишной черты: Арбалетчики будут в точке 3+8.6*12 = 106.2, а Элементали — в точке 10+8*12 = 106. Не зная, кто же именно первым пробежал полный круг, компьютер отдаст ход тому отряду, который окажется дальше от финиша: т.е. Арбалетчикам.
В итоге, как видно из примера, дискретность времени может перевернуть всё с ног на голову: первый ход достанется не тому, кому следовало «по правилам». В общем и целом, от такой дискретности выигрывают более инициативные юниты: у них появляется шанс «незаслуженно» опередить на ход менее шустрые существа.
У дискретности ATB-шкалы есть и ещё одно неприятное следствие: может так сложиться, что два отряда добегут до финиша «одновременно». Если бы в предыдущем примере Арбалетчики стартовали из точки 4 и имели бы инициативу 8.5, то через 12 секунд они бы в точности сравнялись с Огнеными элементалями: 4+8.5*12 = 106. В таких случаях компьютер отдаёт право хода согласно собственному приоритету отрядов на поле. На практике это означает, что мобы получают ход раньше отрядов игроков; а среди отрядов различных игроков приоритет имеют те, чей герой раньше упоминается в протоколе боёв. Например, в дуэли (в случае совпадения позиции на ATB-шкале) отряды левого (красного) игрока будут ходить раньше отрядов правого (синего).
Теперь, ознакомившись с принципами и особенностями ATB-шкалы, можно перейти к более формальному изложению её механики.
Нам придётся ввести несколько понятий и обозначений, чтобы можно было формально описать правила, по которым на ATB-шкалу действуют различные события на поле боя (применение заклинаний, срабатывание спец.способностей юнитов и т.п.). Итак,
Дискретная ATB-шкала в ГВД — это набор точек (делений) на прямой линии. Расстояния между точками измеряется в условных единицах, ATB-метрах (для краткости, будем говорить о просто «метрах»). На ATB-шкале присутствуют все деления с точностью до десятых долей метра: 0, 0.1, 0.2 и т.д. Особыми делениями считаются точка 0 и точка 100. Точка 0 служит началом ATB-шкалы, а достижение точки 100 или любой точки после неё даёт право на ход в игре.
Время на ATB-шкале течёт дискретно, порциями. Минимальная порция времени, которая может пройти между последовательными перемещениями отрядов на шкале, называется ATB-секундой (или просто секундой).
Каждый отряд имеет параметр «Инициатива», который определяет его скорость перемещения по шкале. Например, инициатива 12.5 означает, что за одну ATB-секунду стек проходит 12.5 ATB-метров. В силу дискретности расстояний на шкале, инициатива тоже всегда задаётся с точностью до десятых долей.
С наступлением очередной секунды каждый отряд на ATB-шкале смещается вперёд на расстояние, равное его скорости (инициативе). При достижении или превышении отметки 100 метров отряд получает право хода в игре и смещается назад на 100 метров по шкале. В случае, когда в очередную секунду сразу несколько отрядов оказались за 100-метровой отметкой, они получают право хода в порядке удаления от старта (кто на большей отметке стоит, тот раньше и ходит).
Альтернативные единицы измерения
В жизни мы часто пользуемся различными единицами измерения. Например, в зависимости от обстоятельств, мы мерим скорость либо в м/с (метрах в секунду), либо в км/ч (километрах в час). Также и на ATB-шкале иногда используются единицы измерения, отличные от описанных выше.
Часто расстояние измеряют не в метрах, а в полных ATB-шкалах. 1 ATB-шкала = 100 ATB-метров (это то расстояние, которое надо пройти отряду на шкале, чтобы получить право хода). Ниже мы нигде не будем использовать эту терминологию во избежание путаницы. Но если в какой-нибудь справке или где-нибудь на форуме вы встретите упоминание дробного расстояния на ATB-шкале (например: «сдвиг на 0.5» и т.п.), то знайте, что, скорее всего, подразумевается именно эта единица измерения.
Согласно описанной выше механике, отряд с инициативой 10 пройдёт из точки 0 в точку 100 ровно за 10 секунд. Это время принято называть ATB-туром. 1 ATB-тур = 10 ATB-секунд. В игре это время, как правило, соответствует времени между двумя последовательными ходами героя (т.к. у героя в большинстве случаев инициатива равна 10). ATB-туры используются в первую очередь для измерения времени действия заклинаний.
Соответственно, и скорость существ можно измерять не в ATB-метр/ATB-секунда, а в ATB-шкала/ATB-тур. Заметим, что в таких обозначениях, скорость героя равна единице (одна ATВ-шкала за один ATB-тур). Иногда такую скорость называют «нормальной».
Условные обозначения
Ниже мы будем использовать следующие обозначения:
Пример использования обозначений. Как говорилось выше, сделав свой ход, отряд смещается на 100 метров назад по ATB-шкале: curATB = curATB-100.
5. Начальное положение на шкале
5.1. Начальное расположение отрядов на ATB-шкале
Все стеки существ и герои располагаются в диапазоне от 0 до 10 ATB-метров,
причем только в целых точках (0, 1, …, 10). Это расположение случайно и не зависит от инициативы.
startATB = [0..10]
5.2. Начальное расположение на ATB-шкале вызываемых существ
Фантом
Стартовая позиция фантома на
шкале зависит только от положения героя в момент применения заклинания:
startATB(фантома) = curATB(героя) - 50
Соответственно, фантом попадает в одну из точек диапазона [50..(50+ИНИ_героя)]. Если инициатива героя равна 10, то все фантомы одного героя в отдельно взятом бою будут помещены при вызове в одно и то же положение на шкале.
Призванные из ада
Для вызванного стека устанавливается
тот же начальный разброс на ATB-шкале, какой был у вызывающего:
startATB(Призванный из ада) = startATB(Вызывающий стек).
При этом вызывающий стек, сделав призыв, смещается назад лишь на половину шкалы: curATB = curATB-50
Набеги
Набегающие существа в первой «волне» располагаются в диапазоне [75..85] ATB-метров, во всех остальных
«волнах» располагаются в диапазоне [50..60] ATB-метров (только
целые значения), причем первая «волна» появляется в момент хода
первого стека войск игрока.
startATB = [50..60] ([75..85])
Турниры на выживание и ГН-заговорщики
Существа во всех «волнах»
располагаются в точке 50 метров; причем первая «волна» появляется
в момент хода первого стека войск игрока:
startATB = 50
6.1. Основные игровые механики, влияющие на сдвиги стеков по ATB-шкале:
6.2. Сдвиги героя по шкале
Если герой делает свой ход, то он
смещается на 100 метров: curATB = curATB-100.
Если герой ожидает, то он смещается на 50 метров: curATB = curATB-50.
Способности Дарующий благословение, Дарующий защиту, Повелитель боли, Повелитель проклятий, Повелитель разума, Повелитель ярости
После применения массовых заклинаний герой смещается на 50 метров: curATB = curATB-50.
Способность Духовная связь
После установления связи герой смещается на 50 метров: curATB = curATB-50.
Способность Надзор
Установка надзора смещает героя на 50
метров: curATB = curATB-50.
При срабатывании умения герой отбрасывается на 25 ATB-метров по шкале; при этом
его не может отбросить в отрицательную область: curATB = max(curATB-25; 0).
Способность Сопереживание
Когда у любого из отрядов героя срабатывает положительный боевой дух, герой сдвигается вперед на 10 метров по АТВ-шкале: curATB = curATB+10, когда отрицательный — сдвигается назад: curATB = max(curATB-10; 0).
Способность Чародейство
После использования заклинания герой смещается назад не на 100 метров, а на 90, 80 или 70, в зависимости от уровня изученного навыка (соответственно: начальное, развитое и искусное чародейства). Если герой не использует заклинание, а делает любое другое действие (прямая атака, применение активируемой способности и т.д.), то он после своего хода, как обычно, смещается на 100 метров: curATB = curATB-100. Разумеется, если герой ожидает, то он смещается на 50 метров.
6.3. Сдвиги стеков по шкале от заклинаний и умений героя
Заклинание Осиный рой (у героев)
Вражеский стек отбрасывается по
ATB-шкале на расстояние, зависящее от уровня изучения
магии природы:
curATB = max(curATB-X; 0), где X = 10 при отсутствии навыка; X = 20, 40, 60 при начальной/развитой/искусной магиях природы.
Способность Воодушевление
Смещает стек вперёд на 33 метра: curATB = curATB+33.
Способность Повелитель бурь
Заклинания воздуха отбрасывают
стек по шкале на 30% от пройденного ATB-расстояния: curATB = curATB*0.7
Например, если стек находится в точке 99 (вот-вот получит ход), то его
отбросит в curATB = 99*0.7 = 69.3 — почти на 30 ATB-метров. Если же
стек недавно походил, т.е. его curATB близко к 0, то он, практически, не
изменит своего положения.
Способность Повелитель холода
Заклинания воды останавливают движение стека по шкале на 0.3 ATB-тура
Как мы помним, 1 ATB-тур = 10 ATB-секундам. Получается, что заклинания воды
«замораживают» вражеские отряды на 10*0.3 = 3 секунды. То есть,
ровно три итерации (пока остальные стеки перемещаются на ATB-шкале) этот стек
будет стоять на месте.
Условно эффект такой
«заморозки» можно приравнять к отбросу по ATB-шкале на
расстояние: curATB = curATB-3*Ini, где Ini, напоминаю, это инициатива стека.
Например, для стека с инициативой 20 эффект от заморозки будет равносилен
отбрасыванию по шкале на 60 ATB-метров; а для стека с инициативой 7 —
всего на 21.
Согласно «официальной версии», для заклинания Кольцо холода эффект «заморозки» делится поровну на все стеки, по которым ударило заклинание. На самом же деле, эффект действует только на один стек, который компьютер выбирает по своим внутренним приоритетам (баг, до сих пор не исправленный админами). При этом разделение эффекта происходит всё в той же дискретной манере: если кольцо холода зацепляет лишь один стек, то он замораживается на 3 секунды; если два стека – то на 2 секунды; если три или более стеков – то только на одну секунду.
Умения 'Тяжелый удар' и 'Круговой удар'
Отбрасывают стек на 20 метров: curATB = max(curATB–20; 0).
6.4. Отброс стеков по шкале от умений существ
Атака страхом (Адские жеребцы, Кони преисподней, Кошмары)
Вынуждает отряд сделать незапланированное перемещение по полю и отбрасывает его в самое начало шкалы: curATB = 0.
Оглушающий удар (Латники, Ополченцы, Пехотинцы, Скелеты-воины)
Отбрасывает стек в самое начало шкалы: curATB = 0.
Останавливающий выстрел (Мастера лука, Орки вожди)
Отбрасывает стек на 20 ATB-метров по шкале; как обычно, не может отбросить стек в отрицательную область шкалы: curATB = max(curATB–20; 0).
Отбрасывающий удар (Огры, Огры маги, Огры-ветераны)
Отбрасывает стек в самое начало шкалы: curATB = 0.
Удар лапой (Хозяева медведей)
Отбрасывает стек в самое начало шкалы: curATB = 0.
Усиленная стрела (Лесные снайперы)
Отбрасывает стек в самое начало шкалы: curATB = 0.
В начале статьи были озвучены вопросы, которые рано или поздно возникают у любого игрока, если только он хоть чуть-чуть пытается разобраться в механике боя. Описанные выше принципы ATB-шкалы помогают ответить на многие подобные вопросы. В этом заключительном разделе мы приведём краткий FAQ по ATB-шкале.
7.1. Как отделить единичку так, чтобы она ходила первой?
Увы, это невозможно. Как вы помните, начальный разброс на ATB-шкале совершенно случаен. Однако есть обходные пути решения этой проблемы. На малых уровнях можно отделить от основного стека не одну, а две или три единички; за счёт чего увеличивается вероятность, что один из этих мелких стеков пойдет перед основным (и сможет снять «ответку»). На старших уровнях подобный приём редко допустим. Поэтому игроки используют для снятия «ответки» юнитов другого типа. Например, ТЭ берут с собой ассасина, который ходит перед ящерами; маги — старшего гремлина с миниартом на скорость и инициативу: такой гремлин ходит до стека Джинов; и так далее.
7.2. При какой инициативе мой стек гарантированно опередит противника?
Это не сложно рассчитать. Пусть ваш стек с инициативой Ini1 соревнуется с вражеским стеком с инициативой Ini2; предполагается, что Ini1>Ini2. В худшем случае стартовый разброс поместит вас в точку 0, а противника — в точку 10. Тогда вражеский стек добежит до финиша за 90/Ini2 секунд; вашему же отряду для этого понадобится 100/Ini1 секунд. Отсюда мы получаем условие, гарантирующее вам первенство хода: 100/Ini1 < 90/Ini2, или, что то же самое, Ini1*0.9 > Ini2.
На эту формулу часто (ошибочно) ссылаются, как на «десятипроцентный разброс инициативы в начале боя». Во-первых, как мы знаем, «разбрасывается» не инициатива юнитов, а их стартовое положение на ATB-шкале. Во-вторых, чтобы гарантировано опередить врага 10%-ного прироста к инициативе будет недостаточно. Действительно, потребуется свыше 11%, ведь ту же формулу можно переписать так: Ini1 > Ini2*1.(1).
Заметим, что мы вывели эту формулу исходя из механики непрерывной ATB-шкалы. В случае с дискретной ATB-шкалой ГВД эта формула справедлива лишь наполовину. Т.е., если указанное условие выполнено, то первый стек гарантировано пойдёт раньше второго. Но есть случаи, когда это условие не выполнено, однако первый стек всё равно пойдёт первым при любом стартовом разбросе. К примеру, приоритетный стек с инициативой 10.1 всегда пойдёт раньше неприоритетного стека с инициативой 9.1, хотя заявленное условие не выполняется: 10.1*0.9 = 9.09 < 9.1.
7.3. Какова вероятность опередить другой стек в начале боя?
Этот вопрос резонно вытекает из предыдущего. Пусть условие Ini1*0.9 > Ini2 не выполнено. В этом случае у нас уже нет 100% гарантии, что первый стек опередит второй. Но тогда хочется знать какова вероятность, что он всё-таки пойдёт первым?
В случае непрерывной ATB-шкалы на этот вопрос ответить достаточно легко. На непрерывной шкале вероятность опередить отряд противника зависит только от отношения инициатив отрядов, но не от их абсолютных значений. Пусть отношение этих инициатив равно k = Ini1/Ini2. По сделанным ранее допущениям, 1 < k < 10/9. Тогда вероятность того, что стек с Ini1 пойдёт раньше стека с Ini2, равна 1 - (10-9*k)2/(2*k).
Для дискретной ATB-шкалы, которая используется в ГВД, такой простой формулы не существует. Более того, на дискретной ATB-шкале начинают играть роль такие нюансы, как приоритетность стеков (например, за красного игрока вы играете в дуэли, или за синего). Впрочем, как мы убедимся ниже, для приближённых расчётов «непрерывная» формула вполне годиться.
Хотя формулу для дискретного случая указать нельзя, но на программном уровне вероятность пойти первым определяется довольно легко. Ниже приведена форма для расчёта этой вероятности; вам надо лишь указать инициативы приоритетного (красного) и неприоритетного (синего) отрядов:
Ини1: (приоритетный стек)
Ини2: (неприоритетный стек)
Вероятность для дискретной ATB-шкалы:
54.55%
Вероятность для непрерывной ATB-шкалы: 50%
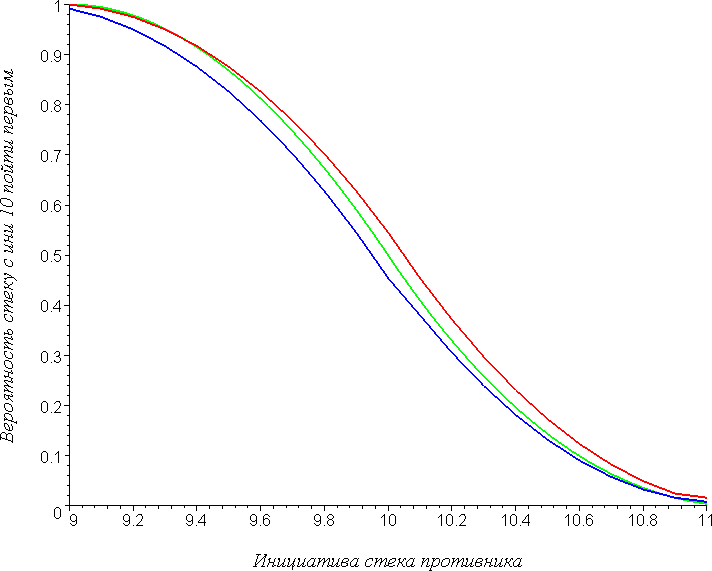
Чтобы было легче представить характер этой формулы, давайте нарисуем поясняющий график. Пусть у нас есть стек с инициативой 10 (таким стеком, как правило, является наш герой). Какова вероятность того, что он пойдёт раньше стека противника? Вот ответ:

По горизонтальной оси отложена инициатива противника, по вертикальной — вероятность опередить его. Зелёная линия соответствует механике непрерывной ATB-шкалы; т.е. это вероятность, которая была бы у нас в 5-х Героях. Красная линия отвечает случаю, когда наш стек является приоритетным на дискретной ATB-шкале (грубо говоря, случай, когда мы играем в ГВД за левого героя в дуэли). Наконец, синяя линия показывает вероятность для неприоритетного стека (соответственно — за правого игрока).
Этот график нельзя назвать характерным. В нём многое — следствие того, что инициатива 10 нацело делит длину ATB-шкалы (100). Например, если за основу взять стек с инициативой 16, то картина будет принципиально другая: график станет ломаным, он будет «скакать» вокруг зелёной линии, и главное, пропадёт всякая зависимость от приоритетности отряда (синяя и красная линии в точности совпадут):
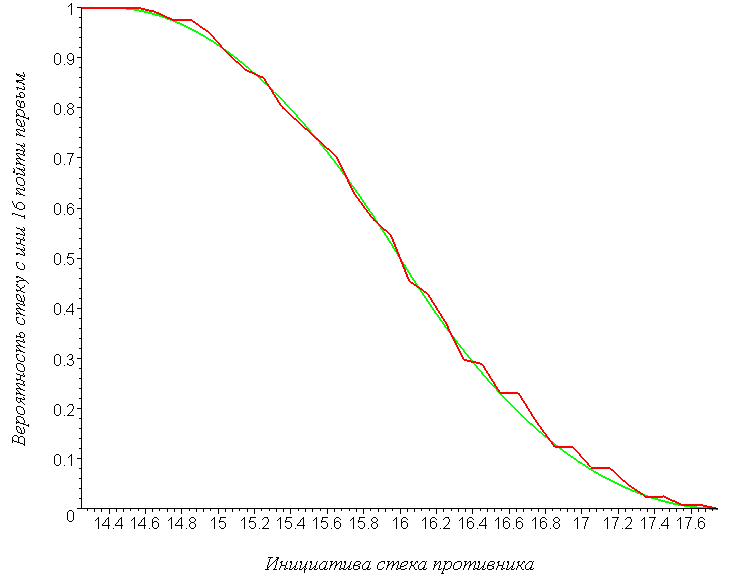
По сути, это противоположная крайность. Для большинства же случаев графики будут чем-то среднем: в каких-то областях приоритетность отряда не будет играть никакой роли; а в каких-то всё же будет оказывать влияние. Для примера можно посмотреть график, в котором шансы опередить противника высчитаны для отряда с инициативой 12:
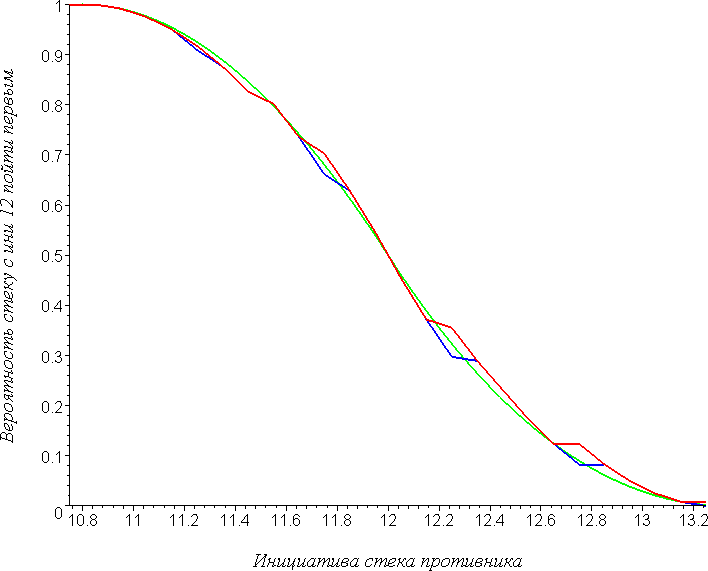
В общей совокупности все эти графики подтверждают высказанную ранее мысль: при общих рассуждениях, когда вычисления делаются приближённо, можно использовать формулу для случая непрерывной ATB-шкалы. Мы воспользуемся этим фактом при ответе на следующий вопрос.
7.4. Насколько полезен бонус ини от ГВ?
Этим вопросом невольно задаёшься после первых поражений от гидрованов. Есть ли смысл ломать арты и тратить нервы в засадах? Чего на деле стоит бонус в 3-4% инициативы? Много это или мало? По сути, ответ содержится в тех графиках, что мы нарисовали в предыдущем пункте. Осталось лишь осмыслить их.
Представим себе дуэль двух эльфов; пусть у одного из них будет 4% бонус инициативы от ГВ, а у другого — нет. Как сильно этот бонус повлияет на шанс первым выстрелить своими лучниками? Базовая инициатива эльфо-лучников равна 10. Бонус 4% от ГВ делает их инициативу равной 10.4. Теперь мы можем воспользоваться формой расчёта вероятности, или же посмотреть на самый первый график из предыдущего пункта. При этом стоит апеллировать к непрерывной «версии» вероятности, т.к. нас интересует общее, «усреднённое», положение дел. Как видим, вероятность того, что отряд с инициативой 10.4 пойдёт раньше отряда с инициативой 10 составляет более 80%! В 4 случаях из 5, а то и чаще, эльф-вор будет выигрывать стрелковую дуэль у своего «честного» противника.
Выше уже говорилось, что на непрерывной ATB-шкале вероятность пойти первым определяется лишь отношением инициатив. Поэтому, будь у нас механика боя непрерывной, тот же самый вывод можно было бы сделать и для дуэли двух орков: у них точно также в 80% случаях первый тапок кинет вороватый варвар.
В случае дискретной ATB-шкалы по отношению инициатив уже нельзя точно определить вероятность одного стека опередить другой. Но, опять же, в среднем, картина принципиально не меняется: стек с бонусом 4% будет примерно в 80% случаях опережать аналогичный стек без этого бонуса.
Стоит отметить, что в этом примере мы не учли бонусы от умелок и артов (мы даже не учли «фракционный» бонус в 3% ини, который есть у всех эльфов). Что изменится, если, допустим, оба эльфа в нашем примере будут иметь бонус к ини в 10% (от умелок, артов и т.д.)? Тогда шансы вора несколько снизятся. Насколько? Давайте посчитаем:
Итак, пусть один стек имеет суммарный бонус в 10% ини, а другой — 14%. Тогда их базовое ини 10 превратится в 11 и 11.4, соответственно. Подставив данные в форму для расчёта вероятности, получим, что теперь стек с большей инициативой будет опережать своего противника в 78.17% случаев.
С повышением общего бонуса инициативы будет снижаться вероятность вора пойти первым. Например, при одинаковом бонусе (от умелок/артов) к ини в 20%, эта вероятность станет 76.29%. А при бонусе в 30%, вероятность опередить визави без 4ГВ будет 74.64%.
Но бонус от артов/умелок в 30% представляется мне верхним потолком для подавляющего большинства боёв в нашей игре. Т.о. получается, что при прочих равных бонусах от артов и умелок, 4ГВ позволит вашему стеку ходить раньше аналогичного стека противника не реже, чем в 3 случаях из 4. Ради такого бонуса не жалко и арты поломать :)
На этом оптимистическом выводе мы завершаем статью о ATB-шкале в ГВД. Надеемся, что она поможет вам лучше разобраться в запутанном механизме боёв.