07.10.2018 15:00
Анализ выхода карт в таверне: Cooldown
Автор: ![]() MOCHET
MOCHET

Важно: Все дальнейшие расчёты и анализы применимы только для игр с одной колодой.

Ситуация такая: Мы выкинули карту, через минимум сколько ходов она придёт к одному или другому игроку на руки? И есть ли некий максимум "не-выхода" карты - может ли карта не выходить 100, 200, 400, 1000, ... ходов ?
Как ход считается любое действие с картой: играть/сбросить; "играем снова" считается как отдельная карта.
Итак, я провёл несколько длительных экспериментов, чтобы получить ответ на этот вопрос. При экспериментах были доступны данные о моих картах и картах противника во время каждого хода (какая карта вышла и какая пришла). Любые запросы/ответы протоколлировались через программу fiddler (перехватчик HTTP запросов) и позже обрабатывались скриптом (statistical language R). Напомню: в колоде у нас 102 карты (ID: 0...101).
У нас есть 3 варианта:
1). 7 против 7 карт
2). 7 против 6 карт
3). 6 против 6 карт
Пример: У меня 7 карт, а у противника 6 карт. Скидываем карту:
I). Первый вопрос:
Через мин. сколько ходов придёт снова карта мне/врагу? (минимальный cooldown)
II). Второй вопрос:
Есть ли верхняя граница "не-получения" карты, то есть может ли карта не выходить подолгу, например 200 ходов?
I). Мин.количество ходов "не-выхода" карты:
1). (102 карты - (7+7))/2 = 88/2 = 44 -> cooldown у сброшенной карты минимум 44 хода.
3). (102 карты - (6+6))/2 = 90/2 = 45 -> cooldown у сброшенной карты минимум 45 ходов.
Теперь интересный случай: 6 против 7:
2). (102 карты - (6+7))/2 = 89/2 = 44.5 -> округление идёт вверх или вниз?
Сделал длительный эксперимент (скидывал карты несколько часов). При втором варианте идёт округление вверх, т.е. cooldown 45 ходов.
II). Есть ли верхняя граница по "не-выпаданию" карты?
Карты могут не выходить по 200, 400 и более ходов. Но вероятность того, что карта будет очень долго не выходить становится крайне мала.
Скрин из анализа эксперимента
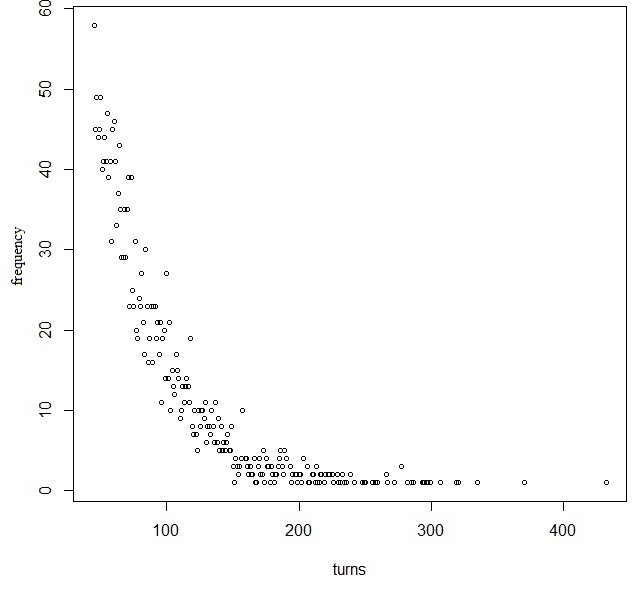
X: "сколько ходов не выпадала карта": turns
Y: "сколько раз происходило данное событие": frequency
На графике видно, что в большинстве случаев карта обязательно выходит где-то после 45-150 ходов. Скорее всего, механизм такой: Скидываем карту, она попадает во вторую часть колоды (в рандомное место). После этого скидываем ещё одну карту, но она может отодвинуть карту до этого, т.е. может получиться, что мы будем постоянно отодвигать одну и ту же карту, не давая ей шанс выйти на руки. Если мы будем играть 10.000 ходов (После этой игры максимальное количество ходов стало 2500), то может получитсья, что одна будет не выходить 1.000 ходов, но исходя, из данных, наблюдаемых в эксперименте вероятность такого события крайне мала.
Формула
Вероятность того, что определённая карта не выйдет из общего котла X ходов: ((44/45)^Х) * 100% [1] (тут я исхожу, что cooldown 45 ходов, т.е. как минимум у одного игрока 7 карт), т.е. будут выходить 44 другие, но не она. X - это количество ходов.
Чем больше X, тем меньше вероятность, что карта останется ещё дольше. Но бывают и случаи, когда бывает что карта не выходит и по 100 или 200 и более ходов. Но случается такое редко.
Данные по формуле [1]:
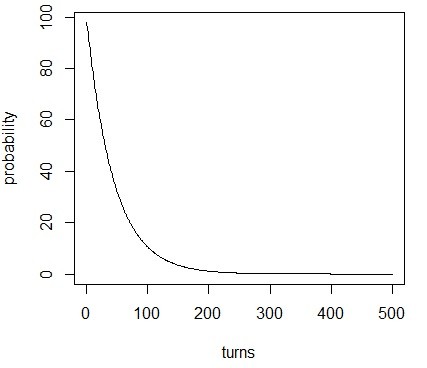
Статистические данные очень схожы с данными рассчитаными по формуле.
В статистических данных у нас частота явлений, а в данных по формуле вероятность.
Чтобы переделать количество явлений (frequency) в вероятность (probability), нужно посчитать сумму всех явлений: N (должно быть меньше чем лимит ходов, т.е. 2500) и делить явления на это число N.
Пример
Событие: 44 хода не выходила карта (любая)
Частота: Это событие было 60 раз
Статистические данные: Всего, например, 2400 собранных явлений.
60/2400*100% - 2.50% вероятность того, что карта выйдет из кулдауна и сразу попадёт кому-то на руки
По формуле: (1-(44/45)^1)*100 = 2.22%
С каждым ходом, пока карта не выходит, вероятность для каждого хода немного падает (прирост становится немного меньше с каждым ходом - в начале как бы самый большой прирост, поэтому и вероятность выше), но в сумме всё равно растёт:
(1-(44/45)^1)*100 = 2.22%
(1-(44/45)^2)*100 = 4.40%
(1-(44/45)^3)*100 = 6.52%
(1-(44/45)^4)*100 = 8.60%
...
(1-(44/45)^100)*100 = 89.43%
99 ходов не выходила - 89.43% вероятность того, что карта выйдет на 100-ый ход, либо 10.57% что не выйдет. Причём здеь нужно учесть, что 100-ый ход после выхода из кулдауна, т.е. если она выйдет на 100-ый ход, а кулдаун был 45 ходов, то карту не будут видеть 99+45 = 144 ходов, а так как большинство игр по правилам столицы около 47 ходов, то эффект кулдауна сводится почти что к нулю, т.е. эффект рандома ещё намного больше усиливается в таких играх, где игры идут слишком быстро, т.е. это вносит тоже свой отдельный вклад в разницу 17% винрейта между первоходящим и вторым игроком.
Прирост
Ход 1: 2.22%
Ход 2: 4.40% - 2.22% = 2.17%
Ход 3: 6.52% - 4.40% = 2.12%
...
-> 2.22% > 2.17% > 2.12% > ... (сравнение вероятностей для каждого хода)
Поэтому вероятность того, что карта попадаёт сразу после выхода из кулдауна самая высокая (- считаем через разницу: 2.22% (Ход 1) - она выше чем у второго хода: 2.17%), а вероятность того, что карта и дальше будет не выходить соответственно падает, но не будет 0%.
Поэтому если вы через 44-45 ходов вам не приходит какая-то карта, то она скорее всего уже у противника.
Итог
Если вам не нравится самая настоящая "рулетка" в играх по правилам столицы (включая и турниры) - играйте в тех районах, где нужна более высокая башня для победы - такие игры продолжаются статистически намного дольше и эффект кулдауна довольно сильно проявляет себя - т.е. там нужно запоминать карты и применять по-настоящему свой скилл. Однако и длятся такие игры намного дольше, поэтому рассчитывайте на 5-10 минут для каждой игры. Если же вам всё же так важно играть по правилам столицы, то тяните время и играйте картами "играем снова" - они накручивают счётчик ходов и вы тем самым можете выловить нужную вам карту.
Итак: Статистически показанно, что игры по правилам столицы чисто для рулетчиков (17% разницы винрейта, невысокая башня для победы и нивелированние эффекта кулдауна) и играть в них крайне глупо.
PHP-Code
PHP code: cooldown
Если описать PHP кодом, то будет примерно вот так:
// здесь сидят карты
$cooldown_array = array(3, 7, 9, 42, 101, ...);
// отсюда вытягиваются карты
$pool_array = array(99, 0, 5, 6, 8, 102, ...);
// у первого игрока 6 карт
$cards_player_1 = 6;
// у второго игрока 7 карт
$cards_player_2 = 7;
// кулдаун 44/45 ходов
$cooldown = ceil((102 - ($cards_player_1 + $cards_player_2)) / 2);
/* Игрок играет картой и получает новую */
// карта с номером 42 будет сидеть 44/45 ходов в этом массиве
$cooldown_array[] = 42;
if(sizeof($cooldown_array) === $cooldown - 1){
// получаем карту, которую засунули 44/45 ходов назад
$card = array_shift($cooldown_array);
// добавляем карту в массив. она готова для выхода в мир
$pool_array[] = $card;
}
// получаем новую карту и даём игроку
$card_id = $pool_array[mt_rand(0, count($pool_array ) - 1)]];
// убираем карту из массива $pool_array
...
метки:
• Механика игры •
• Механика игры •

 Фракции
Фракции









